II-5. Mouvement rectiligne : [MPM]

II-5. Mouvement rectiligne :

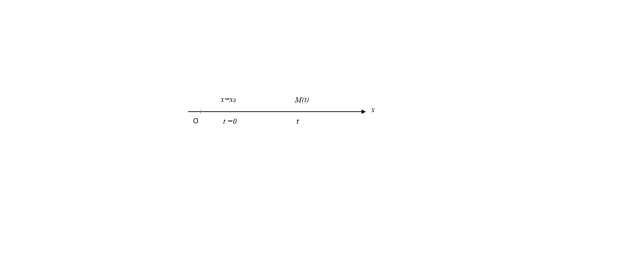
Le mouvement est rectiligne si la trajectoire est une droite.

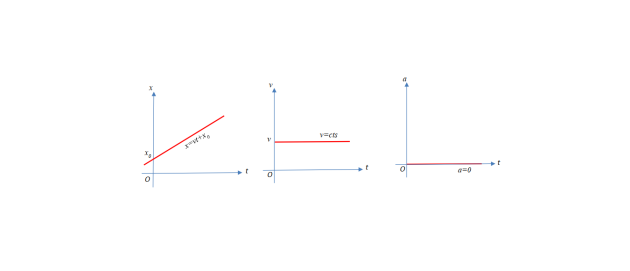
Le mouvement est rectiligne uniforme (MRU) si le mobile garde la même vitesse durant tous son parcours.𝑣 = 𝑐𝑡𝑠 ⟹ 𝑎 = 0

L'équation horaire du mouvement 𝑥 = 𝑓(𝑡)

𝑣 =𝑑𝑥/ 𝑑𝑡 ⟹ 𝑑𝑥 = 𝑣. 𝑑𝑡

\int_{x_{0}}^{x} dx = v \int_{0}^{t} dt

{[x]}_{x_{0}}^{x} = v {[t]}_{0}^{t}

𝑥 − 𝑥₀ = 𝑣(𝑡 − 0)

𝑥 − 𝑥₀ = 𝑣𝑡 ⟹𝑥 = 𝑣𝑡 + 𝑥₀

Condition initiale : pour ⟹ 𝑥 = 𝑥₀

Le Diagramme du mouvement est donné par les équation suivantes :

𝑥 = 𝑓(𝑡)

𝑣 = 𝑔(𝑡)

𝑎 = ℎ(t)

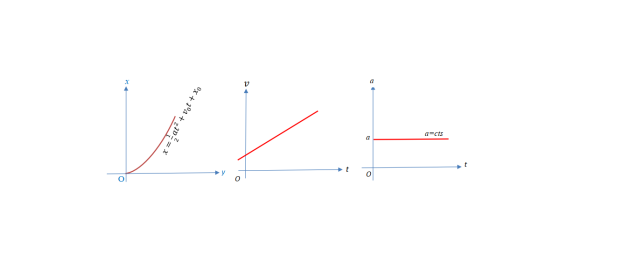
On dit qu'un mouvement est uniformément varié si 𝑎 = 𝑓(𝑡)

𝑎 =𝑑𝑣/𝑑𝑡 ⟹ 𝑑𝑣 = 𝑎 𝑑𝑡

Alors si : à 𝑡 = 0; 𝑣 = 𝑣₀ 𝑒𝑡 𝑥 = 𝑥₀

\int_{v_{0}}^{v} dv = \int_{0}^{t} a dt = a \int_{0}^{t} dt

𝑣 − 𝑣₀ = 𝑎𝑡 ⟹ 𝑣 = 𝑎𝑡 + 𝑣₀

L'équation horaire du mouvement s'écrit :𝑥 = 𝑓(𝑡)

𝑣 =𝑑𝑥/𝑑𝑡 ⟹ 𝑑𝑥 = 𝑣. 𝑑𝑡

\int_{x_{0}}^{x} dx = \int_{0}^{t} v dt = \int_{0}^{t} (at + v_{0}) dt = a \int_{0}^{t} t dt + v_{0} \int_{0}^{t} dt

𝑥 − 𝑥₀ =1/ 2 𝑎𝑡² + 𝑣₀𝑡

⟹ 𝑥 =1/ 2 𝑎𝑡² + 𝑣₀𝑡 + 𝑥₀

On a :

𝑣 = 𝑎𝑡 + 𝑣₀ ⟹ 𝑣 − 𝑣₀ = 𝑎𝑡

𝑣² = (𝑎𝑡 + 𝑣₀)² = (𝑎𝑡)² + (𝑣₀)² + 2𝑎𝑡𝑣₀

⟹ 𝑣² − 𝑣₀² = 𝑎²𝑡² + 2𝑎𝑡𝑣₀

2𝑎 (𝑎/2 𝑡² + 𝑡𝑣₀) ⟹ 𝑣² − 𝑣₀² = 2𝑎(𝑥 − 𝑥₀)