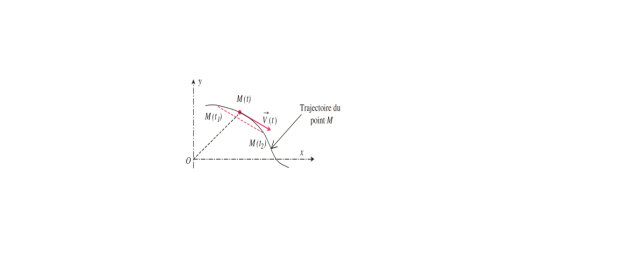
II-3. Vecteur vitesse :

II-3.1 Vitesse moyenne :

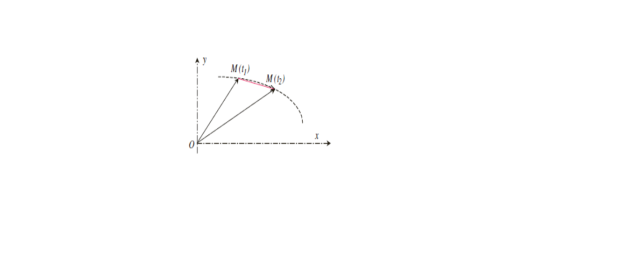
La vitesse d'un mobile est définie comme étant la variation de sa position par rapport au temps.

Soit M la position du mobile à l'instant 𝑑1 qui correspond au point M (𝑑1) = 𝑀1 et à l'instant 𝑑2 au point M (𝑑2) = 𝑀2 avec (𝑑1 < 𝑑2). La vitesse moyenne du mobile entre les deux instants est donnée par :

V moy βƒ— = M 1 M 2 βƒ— Δ t = OM 2 βƒ— − OM 1 βƒ— t 2 − t 1 vec V_{moy} = { widevec { M_{1} M_{2}} } over { %DELTA t}= { widevec { OM_{2}}- widevec {OM} _{1} } over { t_{2}- t_{1}}
Figure 10 : Variation de la position dans le temps : vitesse moyenne.

II-3.2 Vitesse instantanée :

La vitesse instantanée est définie à chaque instant pour les différentes positions du mobile au cours de son mouvement donnée par la relation suivante :

V βƒ— = lim Δ t → 0 V moy βƒ— = dr βƒ— dt = d OM βƒ— dt vec V= lim from{ %Ux0394 t rightarrow 0} vec V_{moy} = { vec dr } over {dt} = {d widevec {OM} } over {dt}

Le vecteur vitesse est toujours tangent à la trajectoire.

Dans un repère cartésien on a :

OM βƒ— = r βƒ— = x ( t ) i βƒ— + y ( t ) j βƒ— + z ( t ) k βƒ— vec OM= vec r =x( t) vec i+y(t) vec j+z(t) vec k )
V βƒ— = dr βƒ— dt = ( dx dt dy dt dz dt ) → | V βƒ— | = ( dx dt ) 2 + ( dy dt ) 2 + ( dz dt ) 2 vec V= { vec dr } over {dt} = left ( stack{ {dx} over {dt} # {dy} over {dt} # {dz} over {dt} } right ) rightarrow lline vec V rline = sqrt{ ( {dx} over {dt} ) ^{2}+ ( {dy} over {dt} ) ^{2}+ ( {dz} over {dt} ) ^{2}}
Figure 11 :Vitesse instantanée