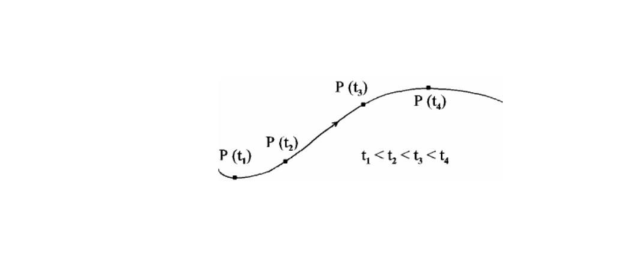
II-2. Vecteur position :

On définit la position d'un point matériel à un instant t par un vecteur 𝑂𝑀 βƒ—βƒ—βƒ—βƒ—βƒ—βƒ— donné par l'équation suivante :

OM βƒ— = r βƒ— = x ( t ) i βƒ— + y ( t ) j βƒ— + z ( t ) k βƒ— vec OM= vec r =x( t) vec i+y(t) vec j+z(t) vec k )

II-2.1 Équation horaire du mouvement :

On appelle équation horaire du mouvement toute équation donnant la position du mobile sur sa trajectoire en fonction du temps.

𝑓(𝑑) = π‘₯

II-2-2 Trajectoire du mouvement :

une trajectoire est l'ensemble des points occupés par le mobile aux temps diffèrent et successifs (voir figure I.1). L'équation de la trajectoire est de la forme :

𝑦 = 𝑓(π‘₯)

Figure 9 : trajectoire d'un mobile aux différentes positions.

Exemple

La position d'un mobile à l'instant est donnée par les équations suivantes :

π‘₯(𝑑) = 2𝑑

𝑦(𝑑) = 0

𝑧(𝑑) = −5𝑑2 + 4𝑑

1- Quelle est la trajectoire du mobile ?

2- Donner le vecteur position à l'instant t=2s.

1-trajectoir du mobile :

π‘₯ = 2𝑑 ⟹ 𝑑 = π‘₯ / 2

𝑧 = −5 (π‘₯/2)2 + 4 (π‘₯ / 2) = −5/4 π‘₯2 + 2π‘₯, la forme de l'équation est une parabole.

2-Le vecteur position :

r βƒ— ( t ) = 2 t i βƒ— + ( − 5 t 2 + 4 t ) k βƒ— vec r(t)= 2t vec i+( -5 t^{2}+4t ) vec k

a l'instant :

r βƒ— ( 2 ) = 4 i βƒ— − 12 k βƒ— vec r( 2 )=4 vec i-12 vec k