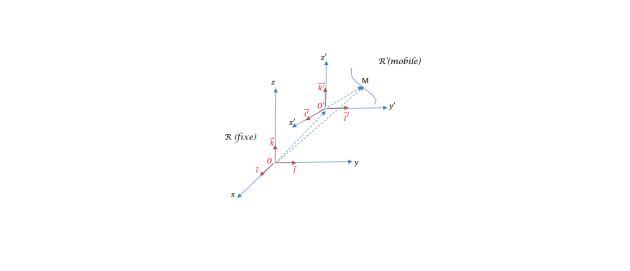
II-7.Mouvements relatifs :
II-7.1. Système de référence :
Soit un point matériel M en mouvement par rapport à un repère mobile R' repéré par un repère de cordonnées (𝑥′, 𝑦′, 𝑧′) dit repère absolu. On peut repérer le même point par rapport au repère fixe R par les coordonnées (𝑥, 𝑦, 𝑧) appelé repère relatif.
D'où on peut écrire 𝑂𝑀 ⃗⃗⃗⃗⃗⃗ = 𝑂 ⃗⃗⃗⃗𝑂⃗⃗⃗′ + 𝑂 ⃗⃗⃗⃗′⃗⃗𝑀⃗
-Le vecteur position dans le repère R : 𝑂𝑀 ⃗⃗⃗⃗⃗⃗ = 𝑥⃗𝑖 + 𝑦⃗𝑗 + 𝑧⃗⃗⃗𝑘 ............repère absolu.
-Le vecteur position dans le repère R' : 𝑂𝑀 ⃗⃗⃗⃗⃗⃗ ′ = 𝑥′ ⃗⃗⃗𝑖′ + 𝑦′⃗𝑗′ + 𝑧′⃗⃗⃗𝑘′......repère relatif
II-7.2. Vecteur vitesse :
𝑎⃗⃗⃗⃗ = 𝑣⃗⃗⃗𝑒 + 𝑣r ⃗⃗⃗
V𝑒⃗⃗⃗ ∶ La vitesse d’entraînement du repère mobile R' par rapport au repère fixe R
V𝑟⃗⃗⃗ : La vitesse relative est la vitesse de M par rapport au repère mobile R'.