II-6. Système de coordonnées.

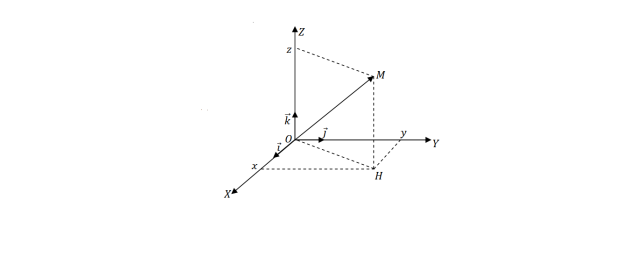
II-6.1. Coordonnées cartésienne

Soit R ( i ⃗ , j ⃗ , k ⃗ ) un repére orthonormé direct d ' origine O et de base ( i ⃗ , j ⃗ , k ⃗ ) Soit R ( widevec {i}, widevec {j}, widevec {k} )un repére orthonormé direct d'origine O et de base ( widevec {i}, widevec {j}, widevec {k} )
Dans la base ( i ⃗ , j ⃗ , k ⃗ ) , ≤ vecteur OM ⃗ se décompose d ' une maniére unique sous la forme : OM ⃗ = x i ⃗ + y j ⃗ + z k ⃗ Dans la base ( widevec {i}, widevec {j} , widevec {k} ), le vecteur widevec {OM} se décompose d'une maniére unique sous la forme: widevec {OM}=x widevec {i}+y widevec {j}+z widevec {k}
Ou ( x , y , z ) sont des composantes du vecteur OM ⃗ dand la base ( i ⃗ , j ⃗ , k ⃗ ) Ou ( x, y, z) sont des composantes du vecteur widevec {OM} ) dand la base ( widevec {i}, widevec {j}, widevec {k} )

x = abscisse de M ; y = ordonnée de M ; z = côte de M.

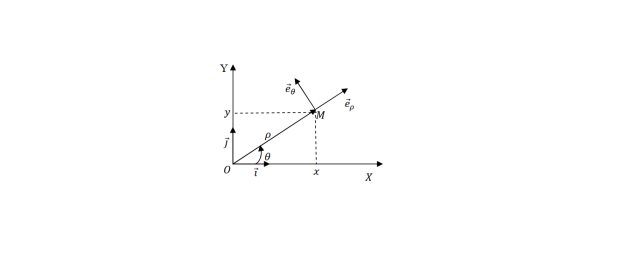
II-6.2. Coordonnées polaires :

Soit ρ = ‖ OM ⃗ ‖ , θ = ( OX ⃗ ^ , OM ⃗ ) Soit %rho = ldline widevec {OM} rdline , %theta = ( hat vec OX, widevec {OM} )

Un point M dans le plan (O X Y) peut être repéré par les données de ( ρ,θ ) appelées coordonnées polaires.

Pour recouvrir tout le plan : 0 ≤ ρ < +∞; 0 ≤ θ < 2π.

- Correspondance avec les coordonnées cartésiennes

( ρ θ ) → ( x y ) : { x = ρ cos θ y = ρ sin θ } ( binom{ %rho }{ %theta } ) toward ( binom{x}{y} ): lbrace binom{x= %rho cos %theta }{y= %rho sin %theta } rbrace

- Base locale associée aux coordonnées cylindriques :

e p ⃗ = cos θ i ⃗ ⃗ + sin θ j ⃗ , e θ ⃗ = − sin θ i ⃗ + cos θ j ⃗ , e z ⃗ = k ⃗ widevec { e_{p}} = cos %theta widevec { widevec {i} }+sin %theta widevec {j}, widevec { e_{ %theta }} = -sin %theta widevec {i}+cos %theta widevec {j} , widevec { e_{z}} = widevec {k}
( e ρ ⃗ , e θ ⃗ , e z ⃗ ˙ ) ( widevec { e_{ %rho }}, widevec { e_{ %theta }}, dot widevec { e_{z}} )

est la base locale associée aux coordonnées cylindriques, c'est une base orthonormée directe.

Dans cette base, le vecteur position s’écrit :

OM ⃗ = ρ e ρ ⃗ + z e z ⃗ widevec {OM}= %rho widevec { e_{ %rho }}+ z widevec { e_{z}}

- Correspondance avec les coordonnées cartésiennes

( ρ θ z ) → ( x y z ) : { x = ρ cos θ y = ρ sin θ z = z } ( stack{ %rho # %theta # z} ) rightarrow ( stack{x # y # z} ): lbrace stack{x= %rho cos %theta # y= %rho sin %theta # z=z} rbrace
( x y z ) → ( ρ θ Z ) : ρ = x 2 + y 2 tg θ = y x Z = Z ( stack{x # y # z} ) rightarrow ( stack{ %rho # %theta # Z} ): stack{ %rho = sqrt{ nospace { x^{2}+ nospace { y^{2}} } } # tg %theta = {y} over {x} # Z=Z}

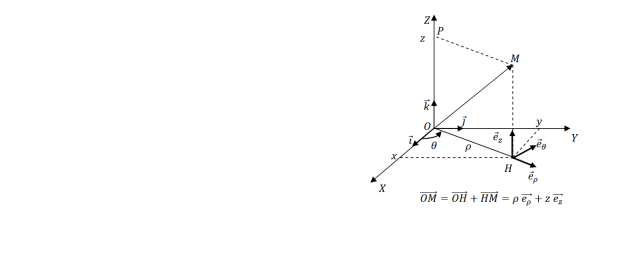
II- 6.3. Coordonnées cylindriques :

Soit H la projection de M sur le plan (OXY)

Le point M est repéré par :

ρ la distance PM ou encore OH;

ρ = ‖ OH ⃗ ‖ = ‖ PM ⃗ ‖ ; %rho = ldline widevec {OH} rdline = ldline widevec {PM} rdline;
ρ = ( OX ⃗ , OH ⃗ ) ^ ; %rho = widehat ( widevec {OX}, widevec {OH} );
z : tel que Z = OP ¯ , z : tel que Z = overline {OP} ,

( ρ, θ, z) sont les coordonnées cylindriques du point M.

ρ est appelé rayon polaire; θ est l'angle polaire et z la cote.

Pour recouvrir tout l'espace : 0 ≤ ρ < +∞; 0 ≤θ < 2π ; –∞ <z< +∞.

-Base locale associée aux coordonnées cylindriques :

( e ρ ⃗ , e θ ⃗ , e z ⃗ ) ( widevec { e_{ %rho }}, widevec { e_{ %theta }}, widevec { e_{z}} )
e ρ ⃗ = cos θ i ⃗ + sin θ j ⃗ widevec { e_{ %rho }} = cos %theta widevec {i} +sin %theta widevec {j}
e θ ⃗ = − sin θ i ⃗ + cos θ j ⃗ widevec { e_{ %theta }}= -sin %theta widevec {i} +cos %theta widevec {j}
e z ⃗ = k ⃗ widevec { e_{z}}= widevec {k}
( e ρ ⃗ , e θ ⃗ , e z ⃗ ) ( widevec { e_{ %rho }}, widevec { e_{ %theta }}, widevec { e_{z}} )

est la base locale associée aux coordonnées cylindriques, c'est une base orthonormée directe.

Dans cette base le vecteur position s'écrit :

OM ⃗ = ρ e ρ ⃗ + z e z ⃗ widevec {OM} = %rho widevec { e_{ %rho }}+z widevec { e_{z}}

- Correspondance avec les coordonnées cartésiennes

( ρ θ Z ) → ( x y z ) : { x = cos θ y = ρ sin θ z = Z } ( stack{ %rho # %theta # Z} ) rightarrow ( stack{x # y # z} ) : lbrace stack{x=cos %theta # y= %rho sin %theta # z =Z} rbrace
( x y z ) → ( ρ θ z ) : { ρ = x 2 + y 2 tg = y x Z = Z } ( stack{x # y # z} ) rightarrow ( stack{ %rho # %theta # z} ): lbrace stack{ %rho = sqrt{ x^{2}+ y^{2}} # tg = {y} over {x} # Z=Z} rbrace

II- 6.4. Coordonnées sphériques :

Soit un point M dans le repère orthonormé direct de la base cartésienne (𝑂, 𝑖, 𝑗, 𝑘⃗ ) qui se déplace selon un système sphérique d'où le repère en

coordonnées sphériques est défini par :(𝑟, 𝜃, 𝜑).

r = ‖ OM ⃗ ‖ = r U r ⃗ r = ldline widevec {OM} rdline = r widevec { U_{r}}

la composante radiale

Le vecteur position 𝑂𝑀 ⃗⃗⃗⃗⃗⃗ est définie par : 𝑟(𝑡), 𝜃(𝑡), 𝜑(𝑡).

En utilisant les relations entre les vecteurs (𝑢 ⃗⃗⃗⃗𝑟 , 𝑢 ⃗⃗⃗⃗𝜃 , 𝑢 ⃗⃗⃗⃗𝜑⃗ ) :

U r ⃗ = sin θ . cos φ i ⃗ + sin θ sin φ j ⃗ + cos j ⃗ widevec { U_{r}}= sin %theta .cos %varphi widevec {i}+sin %theta sin %varphi widevec {j}+cos widevec {j}
U φ ⃗ = − sin φ i ⃗ + cos φ j ⃗ widevec { U_{ %varphi }}=-sin %varphi widevec {i}+cos %varphi widevec {j}
U θ ⃗ = cos θ . cos φ i ⃗ + cos θ . sin φ j ⃗ − sin k ⃗ widevec { U_{ %theta }}=cos %theta .cos %varphi widevec {i}+cos %theta .sin %varphi widevec {j}-sin widevec {k}

Le déplacement élémentaire est défini par :

ds 2 = dr 2 + ( r sin θ . d φ ) 2 + ( r d θ ) 2 , ds^{2}= dr^{2}+ (r sin %theta .d %varphi ) ^{2}+ (r d %theta ) ^{2},

Dérivons le vecteur position en coordonnées sphériques par rapport au temps en trouve le vecteur vitesse

V ⃗ = dr dt = r ˙ U r ⃗ + r U r ˙ ⃗ widevec {V} = {dr} over {dt}= dot r widevec { U_{r}}+r widevec { dot U_{r} }
U r ˙ ⃗ = θ ˙ U θ ⃗ + φ ˙ sin θ U φ ⃗ widevec { dot U_{r} } = dot %theta widevec { U_{ %theta }} + dot %varphi sin %theta widevec { U_{ %varphi }}
U θ ⃗ = cos θ cos φ i ⃗ + cos θ sin φ j ⃗ − son θ k ⃗ . widevec { U_{ %theta }}= cos %theta cos %varphi widevec {i}+cos %theta sin %varphi widevec {j}-son %theta widevec {k} .
U φ ⃗ = − sin φ i ⃗ + cos φ j ⃗ widevec { U_{ %varphi }} =-sin %varphi widevec {i} +cos %varphi widevec {j}

En remplaçant Uθ Uφ dans l'équation de la vitesse 𝑣, on obtient.

𝑣 = 𝑟̇ 𝑢⃗⃗⃗⃗𝑟 + 𝑟 𝜃̇ 𝑢 ⃗⃗⃗⃗𝜃 + (𝑟𝑠𝑖𝑛 𝜑̇) ⃗𝑢⃗⃗⃗𝜑⃗

Alors les trois composantes du vecteur vitesse apparaissent comme suit :

𝑣 = 𝑣⃗⃗⃗𝑟 + 𝑣 ⃗⃗⃗⃗𝜃 + ⃗𝑣⃗⃗𝜑⃗ ⟹ 𝑣 =𝑑𝑟/𝑑𝑡 𝑢 ⃗⃗⃗⃗𝑟 + 𝑟𝑑𝜃/𝑑𝑡 𝑢 ⃗⃗⃗⃗𝜃 + 𝑟𝑠𝑖𝑛𝜃𝑑𝜑/𝑑𝑡 ⃗𝑢⃗⃗⃗𝜑

La base orthogonale directe est constituée des vecteurs (𝑢 ⃗⃗⃗⃗𝑟 , 𝑢 ⃗⃗⃗⃗𝜃 , 𝑢 ⃗⃗⃗⃗𝜑⃗ ) qui dépendent de la position du mobile qui peut être déterminé à partir des équations

horaires r (t), θ (t), φ(t), ce qui nous permet d'établir les composantes 𝑣𝑟, 𝑣𝜃 , 𝑣𝜑 en coordonnée sphériques du vecteur vitesse.

En dérivant toujours l'expression du vecteur vitesse, on obtient l'accélération :

𝑎 =𝑑𝑣/𝑑𝑡 =𝑑/𝑑𝑡 [𝑟̇𝑢 ⃗⃗⃗⃗𝑟 + (𝑟𝑠𝑖𝑛𝜑)𝜃̇𝑢 ⃗⃗⃗⃗𝜃 + 𝑟𝜑̇ 𝑢 ⃗⃗⃗⃗𝜑⃗ ]

a ⃗ = ( r ¨ − r θ 2 ˙ − r φ 2 ˙ sin 2 θ ) U r ⃗ + ( r θ ¨ + 2 r ˙ θ ˙ − r φ 2 ˙ sin θ cos θ ) U θ ⃗ + ( r φ ¨ sin θ + 2 r ˙ φ ˙ sin θ + 2 r φ ˙ θ ˙ cos θ ) U φ ⃗ . widevec {a} =( ddot r-r dot %theta ^{2} -r dot %varphi ^{2} sin^{2} %theta ) widevec { U_{r}}+( r ddot %theta +2 dot r dot %theta -r dot %varphi ^{2}sin %theta cos %theta ) widevec { U_{ %theta }}+( r ddot %varphi sin %theta +2 dot r dot %varphi sin %theta +2r dot %varphi dot %theta cos %theta ) widevec { U_{ %varphi }}.