II-4 Opérations sur les vecteurs
- La somme des vecteurs :
Soit deux vecteurs 𝑉⃗⃗⃗1 et 𝑉⃗⃗⃗2 tel que :
𝑉⃗⃗⃗1 = (𝑥1,y1) ; 𝑉⃗⃗⃗2 = (𝑥2y2)
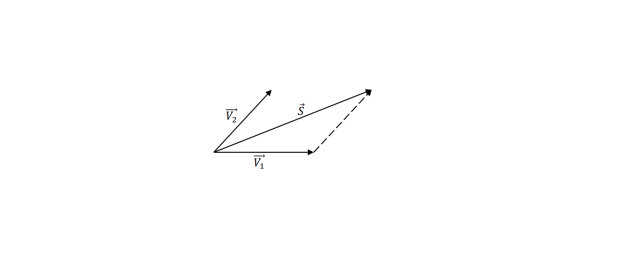
La somme de deux vecteurs est un autre vecteur 𝑆 = 𝑉⃗⃗⃗1 + 𝑉⃗⃗⃗2
Ou par les lois des cosinus :
- Propriétés :
Commutativité :
Associativité :
Distributivité :
La somme d'un vecteur et de son opposé est nulle :
La différence de deux vecteurs :
- La soustraction des vecteurs :
-Le produit scalaire entre deux vecteurs :
Le produit scalaire entre deux vecteurs 𝑉⃗⃗⃗1 et 𝑉⃗⃗⃗2 donne une valeur scalaire.
Si 𝑉⃗⃗⃗1 est parallèle à 𝑉⃗⃗⃗2, donc cos (𝑉 ⃗⃗⃗1, 𝑉⃗⃗⃗2) = 0 et le produit scalaire est nul 𝑉⃗⃗⃗1. 𝑉⃗⃗⃗2 = 0
Si 𝑉⃗⃗⃗1 est perpendiculaire à 𝑉⃗⃗⃗2, donc cos (𝑉⃗⃗⃗1, 𝑉⃗⃗⃗2) = 1 et le produit scalaire 𝑉 ⃗⃗⃗1. 𝑉⃗⃗⃗2 = 𝑉1𝑉2
D'autre part :
Nous avons :
D'où :
𝑉⃗⃗⃗1. 𝑉⃗⃗⃗2 = 𝑥1𝑥2 + 𝑦1𝑦2
-Propriétés du produit scalaire :
Le produit scalaire est commutatif : 𝑉⃗⃗⃗1. 𝑉⃗⃗⃗2 = 𝑉⃗⃗⃗2. 𝑉⃗⃗⃗1
Non associatif : 𝑉⃗⃗⃗1. ( ⃗⃗⃗𝑉⃗⃗⃗2. 𝑉⃗⃗⃗3) donne un vecteur
Distributif : 𝑉 ⃗⃗⃗1. ( ⃗⃗⃗𝑉⃗⃗⃗2 + 𝑉⃗⃗⃗3) = (𝑉⃗⃗⃗1. 𝑉⃗⃗⃗2) + (𝑉⃗⃗⃗1. 𝑉⃗⃗⃗3)
Exemple :
Soit deux vecteur 𝑉⃗⃗⃗1 = 2𝑖 + 3𝑗 − 𝑘⃗ ,⃗⃗ 𝑉⃗⃗⃗2 = 2𝑖 + 2𝑗 − 𝑘
Le produit scalaire 𝑉⃗⃗⃗1. 𝑉⃗⃗⃗2 = 4 + 6 + 1 = 11
- Le produit vectoriel entre deux vecteurs :
Le produit vectoriel entre deux vecteurs 𝑉⃗⃗⃗1 et 𝑉⃗⃗⃗2 est un vecteur perpendiculaire au plan formé par ces deux vecteurs
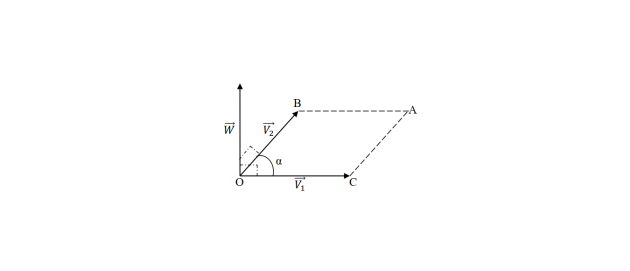
𝑊⃗⃗⃗ = 𝑉⃗⃗⃗1 Λ 𝑉⃗⃗⃗2
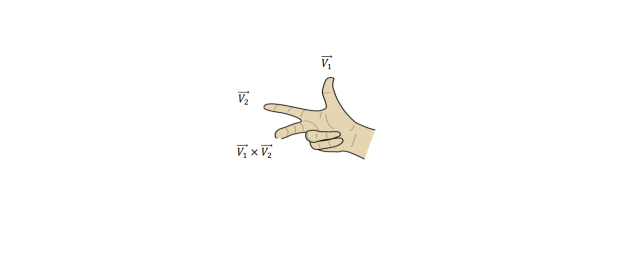
La direction du vecteur 𝑊⃗⃗⃗ est trouvée par la règle des trois doigts de la main droite.
Le module du vecteur 𝑊⃗⃗⃗ est calculé comme suit : 𝑊 = |𝑉⃗⃗⃗1 Λ 𝑉⃗⃗⃗2| = 𝑉1𝑉2 sin (𝑉⃗⃗⃗1, 𝑉⃗⃗⃗2)
Le module du vecteur W représente l'aire du parallélogramme (OABC) formé par les deux vecteurs 𝑉⃗⃗⃗1⃗ 𝑒𝑡⃗⃗𝑉⃗⃗⃗2 (figure 5)
Le produit vectoriel peut être calculé à partir de la méthode du déterminant :
Soit deux vecteurs 𝑉⃗⃗⃗1⃗ , ⃗⃗𝑉⃗⃗⃗2 telle que :
À partir de cette relation, on peut calculer le module de 𝑊⃗⃗⃗ par :
Remarque :
- Propriétés du produit vectoriel :
Non commutatif : 𝑉⃗⃗⃗1 Λ 𝑉⃗⃗⃗2 = −𝑉⃗⃗⃗2 Λ 𝑉⃗⃗⃗1
Non associatif : 𝑉⃗⃗⃗1Λ (𝑉⃗⃗⃗2 Λ 𝑉⃗⃗⃗3) ≠ (𝑉⃗⃗⃗1 Λ 𝑉⃗⃗⃗2)Λ 𝑉⃗⃗⃗3
Distributif : 𝑉 ⃗⃗⃗1 Λ (𝑉⃗⃗⃗2 + 𝑉⃗⃗⃗3) = (𝑉 ⃗⃗⃗1 Λ 𝑉⃗⃗⃗2) + (𝑉⃗⃗⃗1 Λ 𝑉⃗⃗⃗3)
Exemple :
Soit deux vecteurs ⃗⃗𝑉⃗⃗1 = 2𝑖 + 3𝑗 − 5𝑘⃗ ,⃗⃗ 𝑉⃗⃗⃗2 = 2𝑖 + 2𝑗
Le produit vectorielle 𝑊⃗⃗⃗ = 𝑉⃗⃗⃗1 Λ 𝑉⃗⃗⃗2 est :
- Le produit mixte entre trois vecteurs
On définit le produit mixte entre trois vecteurs 𝑉⃗⃗⃗1 , 𝑉⃗⃗⃗2 𝑒𝑡 𝑉⃗⃗⃗3
par le scalaire 𝑉⃗⃗⃗1. (𝑉⃗⃗⃗2 Λ𝑉⃗⃗⃗3) qui est calculé par la méthode du déterminant tel que :
Exemple :
Soit trois vecteurs:
𝑉⃗⃗⃗1. (𝑉⃗⃗⃗2 Λ 𝑉⃗⃗⃗3) = (2.0-2.(-1))2 - (2.0 - 1.(-1))3- (2.2-1.2)(-1)
𝑉⃗⃗⃗1. (𝑉⃗⃗⃗2 Λ 𝑉⃗⃗⃗3) = (2)2 − (1)3 + (2)(−1) = -1
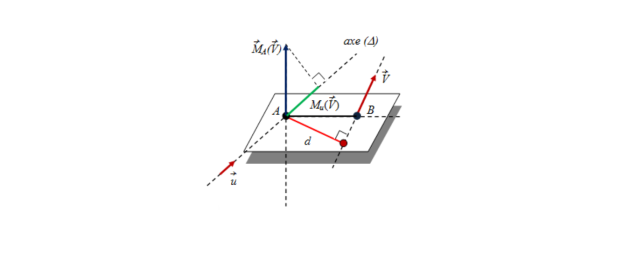
- Moment d'un vecteur par rapport à un point
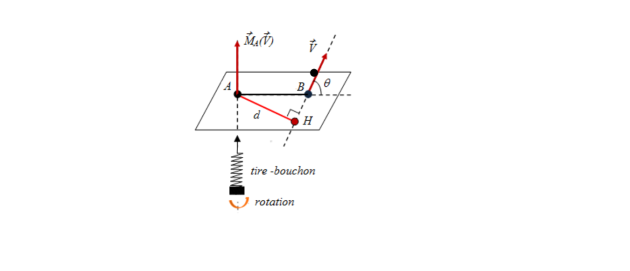
Le moment de vecteur 𝑉⃗⃗⃗1 par rapport au point A est défini par :
Où B est un point quelconque de la ligne d'action de vecteur 𝑉⃗⃗⃗1
De par les propriétés du produit vectoriel, le vecteur moment est perpendiculaire à la fois au
vecteur 𝑉⃗⃗⃗ et au vecteur AB. Son sens est donné par la règle du tourne-vise.