II-3 Composantes d'un vecteur :

Un vecteur est décrit par ces composantes qui sont déterminées à partir d'un repère.

Ce repère peut être linéaire (une seule composante x), plan (deux composantes) ou dans l'espace (trois composantes).

- Cordonnées d'un vecteur dans le repéré cartésien :

Le repère cartésien est un repère orthonormé : les vecteurs unitaires doivent être orthogonaux entre eux et normés à l'unité.

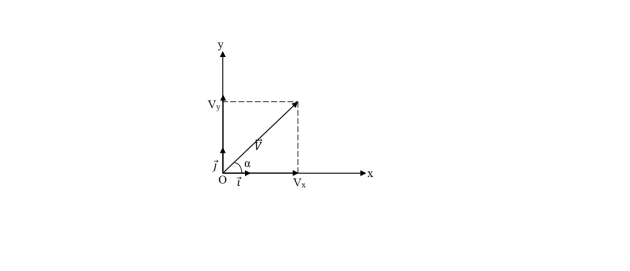
  • Dans le plan (O, π’Š,𝒋) :

vecteur V βƒ— s ' écrit : V βƒ— = V x βƒ— + V y βƒ— vecteur vec V s'écrit: vec V = vec V_{x} + vec V _{y}
avec : V x βƒ— = V x i βƒ— , V y βƒ— = V y j βƒ— avec: vec V_{x}= V_{x} vec i , vec V lsup{} _{y}= V_{y} vec j

𝑉π‘₯= 𝑉 cos 𝛼 ; 𝑉𝑦 = 𝑉 sin 𝛼

Figure 2 : Projection d'un vecteur dans le plan (O, 𝑖,𝑗)

Les composantes du vecteur 𝑉⃗ dans le plan orthonormé (O, 𝑖,𝑗) sont : Vx et Vy et on écrit :

V βƒ— = ( V x V y ) = ( V cos α V sin α ) nospace { vec V } = left ( binom{ V_{x}}{ V_{y}} right ) = left ( binom{V cos %alpha }{V sin %alpha } right )
V βƒ— = V ( cos α i βƒ— + sin α j βƒ— ) vec V = V (cos %alpha vec i + sin %alpha vec j )

Le module du vecteur 𝑉⃗ est calculé à partir de ses cordonnées comme suit :

V = V x 2 + V y 2 V= sqrt{ V^{2}_{x}+ V^{2}_{y}}

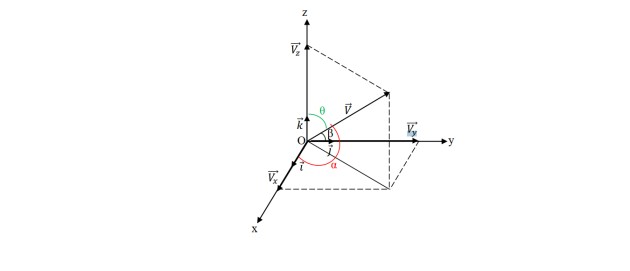
  • Dans l'espace (O, π’Š,𝒋,π’Œ βƒ—βƒ— )

V βƒ— = V x βƒ— + V y βƒ— + V z βƒ— vec V= vec V_{x}+ vec V _{y}+ vec V_{z}

Avec :

V x βƒ— = V x i βƒ— , V y βƒ— = V y j βƒ— , V z βƒ— = V z k βƒ— vec V_{x}= V_{x} vec i , vec V_{y}= V_{y} vec j , vec V _{z}= V_{z} vec k

Vx= V cos α ; Vy= V cos β ; Vz= V cos θ

Figure 3 :Projection d'un vecteur dans l'espace (O, 𝑖,𝑗,π‘˜βƒ— )

Les composantes du vecteur 𝑉⃗ dans l'espace (O, 𝑖,𝑗,π‘˜βƒ— ) sont : Vx , Vy et Vz.

Le module du vecteur 𝑉⃗ est donné comme suit :

V = V x 2 + V y 2 + V z 2 V= sqrt{ V^{2}_{x}+ V^{2}_{y}+ V^{2}_{z}}