Potentiel électrique scalaire
Champ électrique E créé par une charge q en tout point
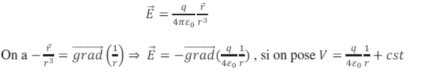
Où V est le potentiel scalaire électrostatique créé par la charge q à la distance r
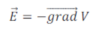
Cette relation montre que le champ électrique dérive d'un potentiel électrique scalaire.
On peut écrire de manière équivalente que le champ électrostatique est à circulation conservative, c'est-à-dire qu'il satisfait la relation intégrale suivante
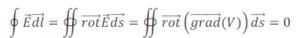
Potentiel électrostatique créé par une distribution discrète de charges
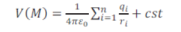
Potentiel électrostatique créé par une distribution linéique de charges
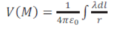
Potentiel électrostatique créé par une distribution surfacique de charges
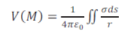
Potentiel électrostatique créé par une distribution volumique de charges
Surfaces équipotentiels
On dit qu'une surface est une surface équipotentielle si le potentiel est le même en tout point de la surface.
Exemple : pour une charge ponctuelle q
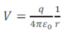
V =cte pour r= cte
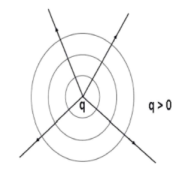
Cet exemple montre que les lignes de champ sont perpendiculaires aux surfaces équipotentielles.