Théorème de Gauss
Le théorème de Gauss exprime la relation entre le flux électrique sortant d'une surface fermée et la somme de charges comprises à l'intérieur du volume délimité par cette surface. On considère une charge ponctuelle q (positive). Cette charge crée un champ électrique d'intensité :
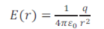
Puis on prend comme surface fermée une sphère de rayon r centrée sur la charge :
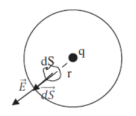
Comme il ya une symétrie (une sphère), tous les vecteurs dS sont radiaux, donc de même direction que E:
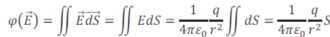
S est la surface de la sphère qui est égale 4πr2
En remplaçant, on trouve :
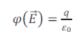
Le flux du champ électrique sortant d'une sphère au centre de laquelle se trouve une charge ponctuelle positive q vaut q/ε0
La relation trouvée par le calcul pour une seule charge et une sphère est valable dans le cas général. Pour une surface fermée renfermant n charges q1, q2, ... , qn.
On peut montrer la relation :
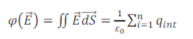
Le flux du champ électrique sortant d'une surface fermée est égal à la somme algébrique des charges comprises dans le volume délimité par la surface, divisée par la permittivité du vide
Si la charge Q est répartie dans l'espace selon une densité volumique de charge ρ nous avons :
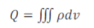
Le théorème de Gauss peut alors s'écrire :
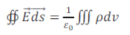
où (s) est une surface fermée quelconque orientée vers l'extérieur et ν est le volume intérieur à (s) . En utilisant le théorème de la divergence, on peut écrire :

on obtient l'équation de Maxwell Gauss électrique qui constitue la forme locale du théorème de Gauss :
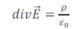
Cette équation relie E aux charges qui constituent les sources du champ électrostatique.