Mouvements d’un corps rigide et transformations homogènes

Introduction

Pour le développement des équations cinématiques du robot manipulateur, il est nécessaire d'établir plusieurs systèmes de coordonnées pour représenter les positions et les orientations de corps rigides. Il est également nécessaire de connaître les transformations de coordonnées entre ces systèmes, afin que les vecteurs représentant des positions, des vitesses et des accélérations, donnés dans un système de coordonnées donné, puissent être représentés dans d'autres systèmes de coordonnées. Dans ce chapitre, nous étudierons les opérations de rotation et de translation entre systèmes de coordonnées tridimensionnelles, en introduisant le concept de transformations homogènes [ 3[1]]

Complément

L'ordre relatif des axes est donné par la règle de la main droite, illustrée dans le tableau suivant

Règle de la main droite pour la formation de systèmes de coordonnées 3D. Le pouce correspond à l’axe des z, l’indicateur à l’axe des x et le majeur à l’axe des y

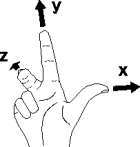
Règle de la main droite : la direction des doigts qui se ferment dans la main indique le sens positif de l'angle de rotation.

Matrice de rotation plane

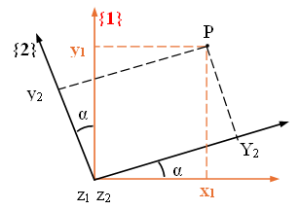
Soit deux repères orthonormés directs partageant la même origine :  et  . On effectue une transformation amenant R1  vers  R2 : rotation d’un angle θ autour de l’axe x puis on exprime le repère  R2  dans le repère  R1 :

·       Rotation (z1,α)

X 1 = cos α x 2 − sin α y 2 + 0 z 2 Y 2 = cos α x 1 − sin α y 2 + 0 z 2 Z 1 = 0 x 1 − 0 y 2 + 1 z 2 [ x 1 y 1 z 1 ] = [ cos α sin α 0 − sin α cos α 0 cos α 0 1 ] ∗ [ x 2 y 2 z 2 ] ⇔ P 1 = R 2 1 × P 2 stack{X_{1}= cos %alpha x_{2}-sin %alpha y_{2}+0z_{2} # Y_{2}= cos %alpha x_{1}-sin %alpha y_{2}+0z_{2} # Z_{1} ` = 0 x_{1} ` ` - ` 0y_{2} ` + ` 1z_{2}} newline newline left [ stack{x_{1} # y_{1} # z_{1}} right ] =left [ stack{cos %alpha # sin %alpha # 0} stack{-sin %alpha # cos%alpha # 0} stack{cos%alpha # 0 # 1} right ]*left [ stack{x_{2} # y_{2} # z_{2}} right ] newline dlrarrow P lsup{1}= R lsup{1}lsub{2}times P lsup{2}

Cette matrice est appelée matrice de rotation, matrice de passage ou matrice de changement de base, Il est possible de définir d'autres rotations rapport aux axes x et y comme suit:

·         Rotation (y1,β)

X 1 = cos β x 2 + 0 y 2 + sin β z 2 Y 1 = 0 x 2 + 1 y 2 + 0 z 2 Z 1 = − sin β x 2 − 0 y 2 + cos β z 2 [ cos β 0 − sin β 0 1 0 sin β 0 cos β ] stack{X_{1}= cos %beta x_{2}+0 y_{2}+sin %beta z_{2} # Y_{1}= 0 x_{2}+1 y_{2}+0z_{2} # Z_{1}= -sin %beta x_{2}-0y_{2}+cos %beta z_{2}}newline newline left [ stack{cos %beta # 0 # -sin %beta} stack{0 # 1 # 0} stack{sin%beta # 0 # cos %beta} right ]

·       Rotation (x,γ)

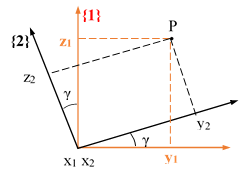
[ 1 0 0 0 cos γ sin γ 0 − sin γ cos γ ] X 1 = 1 x 2 + 0 y 2 + 0 z 2 Y 1 = 0 x 2 + cos γ y 2 − sin γ z 2 Z 1 = 0 x 2 + sin γ y 2 + cos γ z 2 left [ stack{1 # 0 # 0} stack{0# cos%gamma # sin %gamma} stack{0# -sin %gamma # cos%gamma} right ]newline newline stack{X_{1}= 1 x_{2}+0 y_{2}+0z_{2} # Y_{1}= 0 x_{2}+cos %gamma y_{2}-sin %gamma z_{2} # Z_{1}= 0 x_{2}+sin %gamma y_{2}+cos %gamma z_{2}}

Remarque

Orientation déterminée par trois angles : 

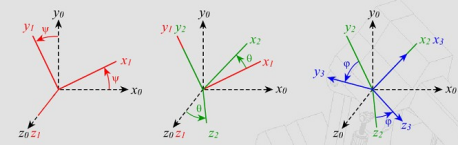
On peut exprimer les trois ddl de rotation de  R3 par rapport à R0 par trois angles.  Pour se faire, on définit  ayant même origine que R0 . R3 peut se déduire  de  R0 par trois rotations successives, en définissant deux repères intermédiaires  R1 et R2.

La première rotation fait passer de  R0 à R1 la seconde de  R1 à  R2 et la troisième de  R2 à  R3 . Ces trois rotations peuvent alors être définies de différentes manières (à condition que  deux rotations consécutives ne soient pas autour du même axe).

Angles d’Euler 

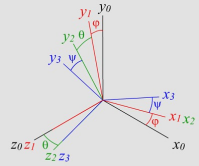
Les angles d’Euler définissent les trois rotations suivantes :

− la précession φ, autour de l’axe z0 fait passer de  R0 à R1

− la nutation θ,  autour de l’axe  x1 , fait passer de  R1 à R2

− la rotation propre ψ,  autour de l’axe, z2 fait passer de  R2 à  R3.

La transformation entre R0 et R3 définie par les angles d’Eleur s’écrit donc :

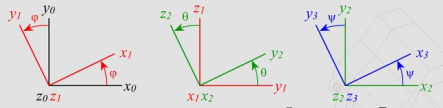
R 3 0 = Rot ( Z 0 , φ ) ∗ Rot ( x 1 , θ ) ∗ Rot ( Z 2 , ψ ) R_{3} lsup{0} =Rot( Z_{0}, %ivarphi)* Rot( x_{1}, %ithêta )* Rot( Z_{2},%ipsi)

− Rotation autour de l’axe z0 d’un angle φ fait passer de  R0 à R1 :

Rot ( Z 0 , φ ) = [ cos α sin α 0 − sin α cos α 0 cos α 0 1 ] Rot( Z_{0}, %ivarphi)=left [ stack{cos %alpha # sin %alpha # 0} stack{-sin %alpha # cos%alpha # 0} stack{cos%alpha # 0 # 1} right ]

− Rotation autour de l’axe x1 d’un angle θ fait passer de  R1 à R2

Rot ( x 1 , θ ) = [ 1 0 0 0 cos θ sin θ 0 − sin θ cos θ ] Rot( x_{1}, %ithêta )=left [ stack{1 # 0 # 0} stack{0# cos%ithêta # sin %ithêta} stack{0# -sin %ithêta # cos%ithêta} right ]

− Rotation autour de l’axe  z2 d’un angle ψ fait passer de  R2 à R3

Rot ( Z 2 , ψ ) = [ cos ψ sin ψ 0 − sin ψ cos ψ 0 co ψ 0 1 ] Rot( Z_{2},%ipsi)=left [ stack{cos %ipsi # sin %ipsi # 0} stack{-sin %ipsi # cos%ipsi # 0} stack{co%ipsi # 0 # 1} right ]

R 3 0 = [ c α c ψ − s φ c θ s ψ s α c ψ + c φ c θ s ψ s θ s ψ − c φ s ψ − s φ c θ c ψ − s φ s ψ + c φ c θ c ψ s θ c ψ s φ s θ − s φ s θ c θ ] R_{3} lsup{0} =left [ stack{c %alpha c%ipsi-s %ivarphi c %ithêta s %ipsi ` ` # s %alpha c%ipsi+c %ivarphi c %ithêta s %ipsi ` ` # s %ithêta s %ipsi} stack{-c %ivarphi s%ipsi-s %ivarphi c %ithêta c %ipsi ` ` # -s %ivarphi s%ipsi+c %ivarphi c %ithêta c %ipsi ` ` # s %ithêta c %ipsi} stack{ ` s %ivarphi s %ithêta # -s %ivarphi s %ithêta # c %ithêta} right ]

Les angles de Roulis et Tangage et Lacet

Ces angles, appelés également angles aéronautiques sont très utilisés dans le domaine  industriel. A la différence des angles d’Eleur, ces trois rotations s’effectuent par rapport à un  référentiel fixe. L’orientation du repère  R3 dans un repère  R0 est donc spécifiée par trois angles : Roulis, Tangage et Lacet. 

φ : Roulis : rotation autour de x0

θ : Tangage : rotation autour de y0

Ψ : Lacet : rotation autour de z0

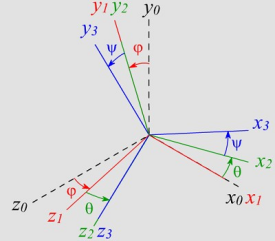
 La transformation entre  R0 et  R3 définie par les angles Roulis Tangage Lacet s’écrit :

R 3 0 = Rot ( Z 0 , ψ ) ∗ Rot ( y 0 , θ ) ∗ Rot ( x 0 , φ ) R_{3} lsup{0} =Rot( Z_{0}, %ipsi)* Rot( y_{0}, %ithêta )* Rot( x_{0},%ivarphi)

R 3 0 = [ cos ψ sin ψ 0 − sin ψ cos ψ 0 0 0 1 ] ∗ [ cos θ 0 − sin θ 0 1 0 sin θ 0 cos θ ] ∗ [ 1 0 0 0 cos φ sin φ 0 − sin φ cos φ ] R_{3} lsup{0} = left [ stack{cos %ipsi # sin %ipsi # 0} stack{-sin %ipsi # cos%ipsi # 0} stack{0 # 0 # 1} right ]*left [ stack{cos %ithêta # 0 # -sin %ithêta} stack{0 # 1 # 0} stack{sin%ithêta # 0 # cos %ithêta} right ]*left [ stack{1 # 0 # 0} stack{0# cos%ivarphi # sin %ivarphi} stack{0# -sin %ivarphi # cos%ivarphi} right ]

R 3 0 = [ c α c ψ − s φ c θ s ψ s α c ψ + c φ c θ s ψ s θ s ψ − c φ s ψ − s φ c θ c ψ − s φ s ψ + c φ c θ c ψ s θ c ψ s φ s θ − s φ s θ c θ ] R_{3} lsup{0} =left [ stack{c %alpha c%ipsi-s %ivarphi c %ithêta s %ipsi ` ` # s %alpha c%ipsi+c %ivarphi c %ithêta s %ipsi ` ` # s %ithêta s %ipsi} stack{-c %ivarphi s%ipsi-s %ivarphi c %ithêta c %ipsi ` ` # -s %ivarphi s%ipsi+c %ivarphi c %ithêta c %ipsi ` ` # s %ithêta c %ipsi} stack{ ` s %ivarphi s %ithêta # -s %ivarphi s %ithêta # c %ithêta} right ]

Transformations homogènes

La représentation d’opérations sous forme matricielle est très intéressante pour simplifier L’écriture. Il serait intéressant de pouvoir inclure aussi les translations sous forme matricielle.

Pour faire cela on introduit les coordonnées homogènes. Il s’agit de former une matrice 4x4 avec la matrice orientation et le vecteur position.

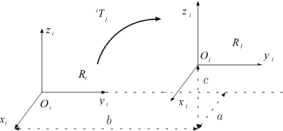
T j i = [ s x s y s z 0 n x n y n z 0 a x a y a z 0 p x p y p z 1 ] = [ R j i P Oj i 0 0 0 1 ] T_{j} lsup{i} =left [stack{ s_{x} # s_{y} # s_{z} # 0} stack{ n _{x} # n_{y} # n_{z} # 0} stack{ a _{x} # a_{y} # a _{z} # 0} stack{p _{x} # p_{y} # p_{z} # 1} right ]= left [ matrix { ` # R_{j} lsup{i} # ` # P_{Oj} lsup{i} ## 0 # 0# 0# 1} right ]

Où :

R j i : R_{j} lsup{i} ` : Matrice (3×3) des rotations donnant l’orientation de Rj dans Ri

P Oj i : P_{Oj} lsup{i} ` : Matrice (3×1) des translations donnant la position de l’origine du repère Rj dans Ri

T j i = [ R j i P Oj i 0 0 0 1 ] = [ I 3 P Oj i 0 0 0 1 ] ∗ [ R j i 0 3 × 1 0 0 0 1 ] T_{j} lsup{i} =left [ matrix { ` # R_{j} lsup{i} # ` # P_{Oj} lsup{i} ## 0 # 0# 0# 1} right ] = left [ matrix { ` # I_{3} # ` # P_{Oj} lsup{i} ## 0 # 0# 0# 1} right ]*left [ matrix { ` # R_{j} lsup{i} # ` # 0_{ 3 times 1 } ## 0 # 0# 0# 1} right ]

Matrice de transformation homogène de translation pure

Lorsque deux repères sont uniquement liés par une translation, il est possible de passer de  l’un à l’autre en utilisant une matrice de transformation homogène de translation pure. Soit deux repères  Ri et Rj de même base, ayant comme origines, les deux points Oi et Oj respectivement.Considérons une translation composée de :

− d’une translation a selon l’axe x

− d’une translation b selon l’axe y

− d’une translation c selon l’axe z    

Cette translation est exprimée par :

T j i = Trans ( x , a ) ∗ Trans ( y , b ) ∗ Trans ( z , c ) T_{j} lsup{i} =Trans( x, a)* Trans( y, b )* Trans( z,c)

Transformation par rapport à un référentiel mobile

Soit les deux référentiels Ra et Rb . Puisque nous allons considérer que nous connaissons la

description du référentiel Rb par rapport au référentiel Ra , c’est-à-dire la matrice de transformation homogène T a b T_{a} lsup{b} , nous pouvons considérer le référentiel Ra comme étant fixe et le référentiel Rb comme étant mobile.

La description d’un référentiel Rc par rapport au référentiel Ra, obtenue en appliquant une

Transformation T par rapport au référentiel Rb est définie par:

T j i = T b a ∗ T T_{j} lsup{i}=T_{b} lsup{a}*T

Transformation par rapport au référentiel fixe

On cherche à trouver la description, par rapport au référentiel Ra , d’un référentiel

Rc obtenu en appliquant une transformation T par rapport au référentiel Ra. Cette

description est définie par:

T j i = T ∗ T b a T_{j} lsup{i}=T*T_{b} lsup{a}