Équation de continuité (forme différentielle)
Mathématiquement, elle est représentée, comme étant le taux de variation de masse d'un système est nul. Par définition, un système = quantité de masse fixe.
Considérons un élément fluide parallélépipédique de volume dV=dxdydz incompressible au repos [5][1].

L'équation de continuité stipule que ; un système = quantité de masse fixe. Ce qui nous permis d'écrire :
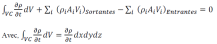
Essayons de développer les termes de l'équation ci-dessus suivant les trois axes ox, oy et oz. Pendant le temps dt, il entre par la face dydz un débit massique de fluide égale à :
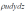
Pendant le même temps, il sort part la face opposée dydz, un flux massique de fluide égale à celui qui est entré, augmenté de sa différentielle partielle par rapport à x. or seules les grandeurs peuvent varier suivant x. le débit massique sortant est donc :
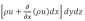
La différence de ces deux termes donne :
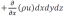
Qui représente la variation (augmentation) du débit massique traversant le parallélépipède. Par un raisonnement similaire, on peut déterminer la variation en débit à travers les autres faces.
Les résultats obtenus sont regroupés dans le tableau

L'équation de continuité devient :
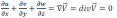
C'est la forme recherchée de l'équation de conservation de masse pour un volume de contrôle infinitésimal dans un système de coordonnées cartésiennes.
Elle est applicable aux principales catégories d'écoulement, visqueux, non visqueux, pour fluide incompressible, ou un fluide compressible. Souvent appelée équation de continuité car elle ne nécessite aucune hypothèse, sauf le fait que la densité et la vitesse sont des fonctions continues.