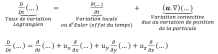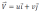Description de mouvement de fluide
Rappel :
Le terme fluide désigne un comportement qui s'oppose au comportement élastique ou plastique associé aux solides. Par définition, on dit que la matière est fluide lorsqu'elle se déforme aussi longtemps que lui sont appliquées des contraintes tangentielles. En termes simples on peut dire qu'un fluide coule quand un solide se déforme
Attention :
Si le référentiel n'est pas galiléen, il suffit d'ajouter dans le bilan des forces, les forces volumiques d'inertie.
Approche Lagrangienne
Identifier (ou étiqueter) une particule fluide ; suivez-la au fur et à mesure qu'elle se déplace et surveillez les changements dans ses propriétés. Les propriétés peuvent être la vitesse, la
température, la densité, la masse ou la concentration, etc. dans le champ d'écoulement.
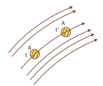
Reportez-vous à la figure ci-dessus. La particule fluide «A» au moment t a été déplacé vers un autre emplacement au moment t'. Sa propriété, par exemple la vitesse, est enregistrée lorsque la particule se déplace dans le champ d'écoulement :
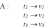
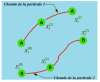
Notez que les vitesses enregistrées sont associées à la même particule de fluide, mais à des endroits différents et à des moments différents.
Imaginez un capteur de vitesse fixé sur un oiseau, volant dans l'atmosphère et enregistrant la vitesse de l'oiseau dans le champ d'écoulement.

Dans ce cas, le capteur enregistre les données de vitesse suivantes :
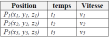
Le changement temporel de la vitesse dans une telle mesure est désigné par :
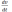
Appelé dérivé matériel ou dérivé substantiel. Il reflète le changement temporel de la vitesse (ou de toute autre propriété) de la particule fluide marquée (ciblée), observée par un observateur se déplaçant avec la particule fluide. L'approche lagrangienne est également appelée «approche basée sur la particule».
Exemple :
L'écoulement est suivi par un observateur depuis une position fixe. C'est le cas, par exemple, d'un atterrisseur sur Mars fixé au sol qui mesure la vitesse du vent, la température, ou la pression. Cette description est souvent préférée car elle est la plus pratique.
Approche Eulérienne
Identifiez (ou étiquetez) un certain emplacement fixe dans le champ d'écoulement et suivez l'évolution de sa propriété, à mesure que différentes particules passent par cet emplacement.
Dans ce cas, la propriété suivante, par exemple, la température est enregistrée par le capteur :
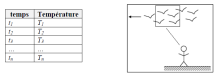
Notez que les températures enregistrées sont associées à l'emplacement fixe dans le champ d'écoulement, ayant différents particules fluide à différents moments.
Disons que nous sommes intéressés par le taux de variation temporelle du changement de température, T, que la particule observe lorsqu'elle se déplace d'un endroit à l'autre. La particule peut subir un changement de température car la température de tout le champ de fluide peut changer en fonction du temps (c'est-à-dire que le champ de température peut être instable).
De plus, le champ de température peut avoir des gradients spatiaux (différentes températures à différents endroits, c'est-à-dire non uniformes), de sorte que lorsque la particule se déplace d'un point à l'autre, elle subit un changement de température.
Ainsi, la particule subit deux effets qui peuvent provoquer un changement de température dans le temps : les effets instables, également appelés effets locaux ou eulériens, et les effets de gradient spatial, également appelés effets de convection. Nous pouvons décrire cela en termes mathématiques en écrivant la température de tout le champ en fonction du temps, t et de l'emplacement, x :
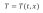
Notez que l'emplacement de la particule de fluide est fonction du temps : x = x (t) de sorte que :
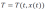
Prendre la dérivée temporelle de la température, étendre le vecteur de localisation en ses composantes x, y et z et utiliser la règle de chaîne donne :
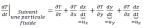
Récrivant cela sous une forme plus compacte :
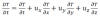
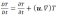
La notation, D/Dt, indiquant une dérivée lagrangienne (parfois désigne un élément matériel ou, (substantiel), est utilisée dans l'éq. Précédente pour indiquer que nous suivons un élément
(morceau) de fluide particulier et non pas une particule seulement. Plus généralement, nous avons :