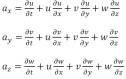Champ de vitesse et champ d'accélération
Remarque :
la vitesse 𝑣 en mécanique des fluides désigne la norme du vecteur vitesse d'une particule de fluide.
En conséquence on peut avoir 𝑣(M) =0 bien que la vitesse moyenne d'une molécule soit non nulle
Sur la base du concept du milieu continu qu'on a accordé au fluide, la description des propriétés du fluide (densité, pression, vitesse, accélération etc. ...) peuvent être des fonctions de l'espace, et peuvent par conséquence être représentées graphiquement.
Une de ces grandeurs est le champ de vitesse. Il s'agit d'une fonction vectorielle de la position et du temps avec les composantes u, v et w. Dans un système Eulérien, la formulation du vecteur de vitesse en coordonnées cartésiennes est définie comme :
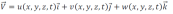
La dérivée totale par rapport au temps du vecteur de vitesse est le vecteur d'accélération:

Pour la composante de vitesse u, on peut écrire :
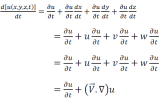
De même pour les composantes v et w, on a :
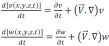
Sommons les trois termes précédents, on écrit :
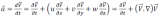
Il vient donc :