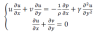Définitions et caractéristiques de la couche limite
Définition :
La couche limite est la zone d'interface entre un corps et le fluide environnant lors d'un mouvement relatif entre les deux. Elle est la conséquence de la viscosité du fluide et est un élément important en mécanique des fluides (aérodynamique, hydrodynamique), en météorologie, en océanographie, etc.
L'écoulement d'un fluide visqueux sur une paroi solide représente une région dans laquelle la vitesse augmente de zéro à la paroi et s'approche de la vitesse de l'écoulement libre. Cette région s'appelle la couche limite.
La figure 2.1 montre le développement d'une couche limite sur un côté d'une longue plaque plane parallèle au sens de l'écoulement.
Le gradient de vitesse provoque une contrainte de cisaillement importante au niveau de la paroi τo (ou τw). Comme le montre la figure 2.1 :
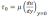
Le gradient de vitesse dans la couche limite turbulente est plus grand que celui dans la couche limite laminaire.
* Une région d'entrée où la couche limite se développe , la pression est constante,
* Une région ou l'écoulement est complètement établi où :
La couche limite remplit toute la zone d'écoulement.
Les profils de vitesse, le gradient de pression, et la contrainte de cisaillement sont constants ; c'est-à-dire qu'ils ne sont pas en fonction de (x),
L'écoulement est soit laminaire, soit turbulent sur toute la longueur de l'écoulement, c'est-à-dire que la phase de transition n'est pas prise en compte.
Cependant, les caractéristiques de la couche limite d'écoulement visqueux pour les écoulements externes sont comme indiqué ci-dessous pour l'écoulement sur une plaque plane :
Considérons un écoulement sur une plaque plane, comme illustré à la figure 2.1.
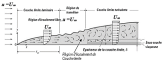
L'écoulement sur la plaque peut être divisé en deux domaines.
i) 0 ≤ y ≤ δ écoulement de couche limite dans laquelle l'effet de force visqueuse est important.
En raison de la condition de non-glissement à la paroi, la première couche de fluide subit un retardement. Cette couche retardée provoque un retard supplémentaire pour la couche adjacente, développant ainsi une région mince dans laquelle la vitesse d'écoulement augmente de zéro à la paroi solide et se rapproche de la vitesse de l'écoulement libre.
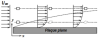
En raison de la présence d'un gradient de vitesse à l'intérieur de la région de la couche limite, les particules fluides au sommet commencent à se déformer, lesquelles ont une vitesse supérieure à celle se trouvant en bas. Cette force provoque la rotation de la particule fluide lorsqu'elle pénètre dans la région de la couche limite (voir la figure 2.2). Par conséquent, cette couche de fluide est appelée également écoulement rotationnel.
ii) y > δ : Zone d'écoulement externe à la couche limite où la force visqueuse est très faible et peut être négligée. Il n'y a pas de gradient de vitesse dans cette zone et la particule fluide ne fait pas de rotation lorsqu'elle entrera dans la région extérieure à la couche limite. Par conséquent, l'écoulement est également appelé écoulement irrotationnel.
Comme le montre la figure, les conditions de la couche limite sont que le fluide adhère à la paroi solide.
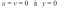
Et à l'extérieur de la couche limite, la vitesse du fluide est égale à la vitesse de l'écoulement libre, c'est-à-dire :
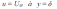
La condition à la limite suivante est également valable pour l'écoulement de couche limite,
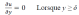
Ceci indique que la distribution de la vitesse est uniforme dans la direction y à l'extérieur de la zone de couche limite.
Épaisseur de couche limite
On distingue trois types d'épaisseur de couche limite, à savoir :
Épaisseur conventionnelle de la couche limite, δ
Épaisseur de déplacement de la couche limite, δ*
Épaisseur du moment de la couche limite, θ
L'épaisseur de la couche limite est définie comme la distance verticale entre la paroi solide et le point où la vitesse de l'écoulement atteint 99% (u=0.99 U ) de la vitesse de l'écoulement libre
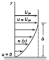
Épaisseur de déplacement de la couche limite, δ*
L'épaisseur de déplacement représente la distance verticale dans laquelle la paroi solide doit être déplacée vers le haut de sorte que le fluide réel ait le même débit massique que le fluide idéal.
Considérons deux types d'écoulement de fluide sur une plaque plane horizontale fixe avec une vitesse d'écoulement , comme illustré à la figure 2.4.
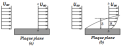
En l'absence de viscosité dans le cas d'un fluide parfait (Figure 2.4 (a)), un profil de vitesse uniforme est développé au-dessus de la paroi solide. Cependant, dans le cas de fluide visqueux (fluide réel) et pas de glissement sur la paroi, un gradient de vitesse est développé dans la région de la couche limite, comme le montre la figure 2.4 (b).
Épaisseur de quantité de mouvement de la couche limite, θ
Une autre épaisseur de la couche limite, il s'agit de l'épaisseur de quantité de mouvement, elle serve à prédire la force de traînée sur la surface de l'objet (Fig.2.6).

Équations de la couche limite
Tout d'abord, on résume les principales hypothèses que nous nous sommes déjà fixées sur l'écoulement considéré.
écoulement laminaire, permanent, bidimensionnel dans le plan (Oxy).
fluide incompressible
L'écoulement est donc décrit par les équations de Navier-Stokes ainsi que l'équation de continuité, comme suit :
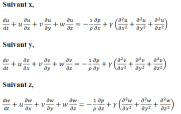
Sous forme vectorielle, elles peuvent être réécrites sous la forme :
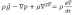
L'équation de continuité est :
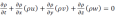
Compte tenu des hypothèses fixées ci-dessus, pour l'écoulement dans la couche limite. Par conséquent, les équations de Navier-Stokes et celle de continuité de l'écoulement du fluide sont réduites à :